Il suffit de trouver \(\alpha\) en radian et sous forme fractionnaire.
\documentclass[border=5mm]{standalone}
\usepackage{tkz-euclide}
\usetkzobj{all}
\begin{document}
\begin{tikzpicture}
\tkzDefPoint(0,0){O}
\foreach[count=\i] \ANG in {22.5,67.5,112.5,157.5,202.5,247.5,292.5,337.5}
{
\tkzDefPoint({5*cos(\ANG*pi/180)},{5*sin(\ANG*pi/180)}){P\i}
}
\tkzDrawPoints[color=red,fill=white,size=7](P1,P2,P3,P4,P5,P6,P7,P8)
\tkzInterLL(P1,P8)(P6,P7) \tkzGetPoint{I}
\tkzDefSquare(P1,I) \tkzGetPoints{C}{D}
\tkzDrawPolygon[color=black,ultra thick](P1,D,C,I)
\tkzDrawPolygon[color=magenta, ultra thick](P7,P8,C)
\tkzDrawPolygon[color=red,ultra thick](P1,P2,P3,P4,P5,P6,P7,P8)
\tkzMarkAngle[fill=magenta!35,size=2.8cm,opacity=.5](P8,C,P7)
\tkzLabelAngle[pos = 2.3](P8,C,P7){\color{black}{\mbox{\Large$\alpha$}}}
\end{tikzpicture}
\end{document}

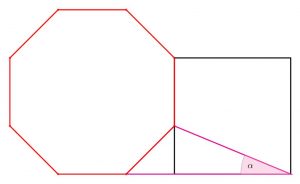
Soit \(a\in \mathbb{R}^+_0\) la longueur du côté de l’octogone.
La longueur du côté du carré vaut : \(\frac{2+\sqrt{2}}{2}a\)
On en déduit : \(\tan\alpha = \sqrt{2} – 1\)
Il reste à trouver la valeur fractionnaire (en fonction de pi) de \(\arctan \left( \sqrt{2} – 1 \right)\)
Une autre piste