Dans un carré de côté 1, on trace un carré dont les sommets sont situés au tiers des côtés du carré initial, et on répète indéfiniment l’opération. On demande de calculer la longueur de la spirale dont les premiers segments sont tracés en rouge ci-contre.
Fichier pdf – Source latex de la figure.
Il faut reprendre cette figure en ne dessinant que les premières itérations de sa construction. Cela permettra plus facilement de définir les différentes variables à mettre en relation.
Par ailleurs, la configuration géométrique du problème laisse penser qu’une suite géométrique se cache derrière le processus de raisonnement permettant d’aboutir à la solution finale.
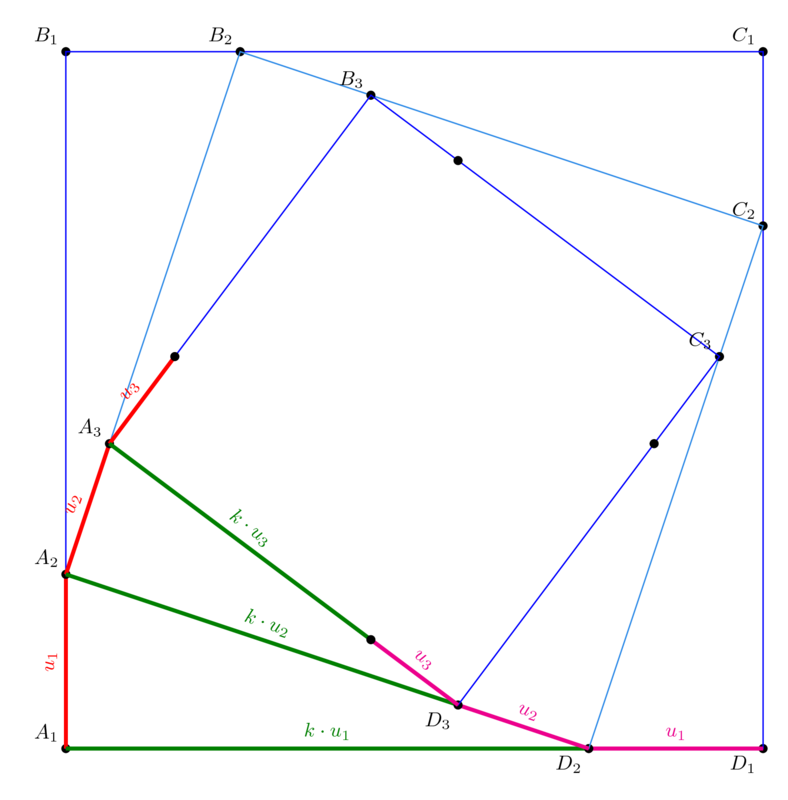
On définit les sommets des carrés emboîtés par les lettres A,B,C et D. Plus précisément, en numérotant chaque carré, le carré numéro \(i\) aura pour sommets les points \(A_i\), \(B_i\), \(C_i\) et \(D_i\).
La longueur de la spirale rouge après n itérations est déterminée par \(L_n = \sum\limits_{i=1}^{n} u_i\)
Bon d’accord, mais que valent les \(u_i\) ? Comment les calculer ? Pour commencer notre investigation, on s’intéresse aux triangles rectangles \(A_iA_{i+1}D_{i+1}\) pour y trouver une relation entre \(u_{i+1}\) et \(u_{i}\). On trouve :
$$\left(\left(1+k\right)\cdot u_{i+1}\right)^2 = \left( 1+k^2\right) \cdot u_i^2 $$
avec \(k=\frac{1}{u_1}-1\)
Comme \(u_{i}>0\), on a : $$u_{i+1}=\frac{\sqrt{1+k^2}}{1+k} \cdot u_{i}$$
Les \(u_{i}\) sont par conséquent les termes d’une suite géométrique de premier terme \(u_{i}\) et de raison \(q =\frac{\sqrt{1+k^2}}{1+k}\)
Remarque : on a aussi \(q =\sqrt{2 \cdot u_1^2-2 \cdot u_1+1}\)
La somme des n premiers termes d’une suite géométrique est donnée par $$S_n=u_1\cdot\frac{1-q^{n}}{1-q} \text{ avec } q\neq 1$$
On applique cette formule en reprenant les données de l’énoncé : \(u_1=1/3\) et donc \(k=2\)
$$L_n = \frac13 \cdot \frac{1-\left(\frac{\sqrt{5}}{3}\right)^n}{1-\frac{\sqrt{5}}{3}}$$
Comme la raison de cette suite est comprise entre -1 et 1, \(L_n\) converge vers $$L=\frac13 \cdot \frac{1}{1-\frac{\sqrt{5}}{3}} = \frac{3+\sqrt{5}}{4}$$
La spirale infinie rouge est donc de longueur finie \(\frac{3+\sqrt{5}}{4}\)