Une grenouille se trouve devant un escalier de 20 marches. Sachant qu’elle peut gravir soit une, soit deux marches à la fois, combien de solutions possibles y-a-t il pour gravir l’escalier ?
On considère un escalier comprenant \(n\) marches puis on note \(u_n\) le nombre de façons différentes pour gravir cet escalier.
Si \(n=0\) alors \(u_0=1\) puisqu’il n’y a qu’une seule possibilité : rester sur place !
Si \(n=1\), un seul bond possible pour le batracien et donc une seule possibilité : on a \(u_1=1\).
Soit maintenant un escalier comportant \(n+2\) marches. Par hypothèse, son avant dernier bon était ou bien un bond d’une marche ou bien un bond de deux marches.
Cela donne donc deux éventualités disjointes que l’on va dénombrer séparément et qu’il suffira ensuite d’ajouter pour avoir la réponse définitive.
Si c’était un bond d’une marche, c’est qu’alors elle avait gravi jusque là \(n+1\) marches de \(u_{n+1}\) façons différentes.
Si c’était un bond de deux marches, c’est qu’alors elle avait gravi jusque là \(n\) marches de \(u_n\) façons différentes.
On obtient donc \(u_{n+2}=u_{n+1}+u_n\).
On reconnait aisément la célèbre suite de Fibonacci dont on peut calculer les termes de proche en proche à partir de la formule de récurrence \(F_{n+2}=F_{n+1}+F_n\) à partir des termes initiaux \(F_1=1\) et \(F_2=1\).
On obtient ainsi \(u_{20}=F_{21}=10946\). Ce qui donne 10946 possibilités pour cette courageuse grenouille.
Illustration pour 4 marches :
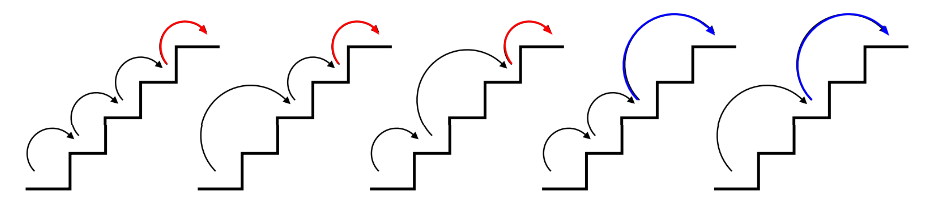
Tableau récapitulatif :
| Nombre de marches | Liste des solutions | Nombre de solutions | Fibonacci |
| 0 | \(\emptyset\) | 1 | \(u_{0}=F_{1}=1\) |
| 1 | {1} | 1 | \(u_{1}=F_{2}=1\) |
| 2 | {1,1},{2} | 2 | \(u_{2}=F_{3}=2\) |
| 3 | {1,1,1},{1,2},{2,1} | 3 | \(u_{3}=F_{4}=3\) |
| 4 | {1,1,1,1},{2,1,1},{1,2,1},{1,1,2},{2,2} | 5 | \(u_{4}=F_{5}=5\) |
| 20 | ………. | 10946 | \(u_{20}=F_{21}=10946\) |
